Solar Eclipse Prime Page

Annular Solar Eclipse of -1836 Mar 12 (1837 Mar 12 BCE)

Fred Espenak

Introduction

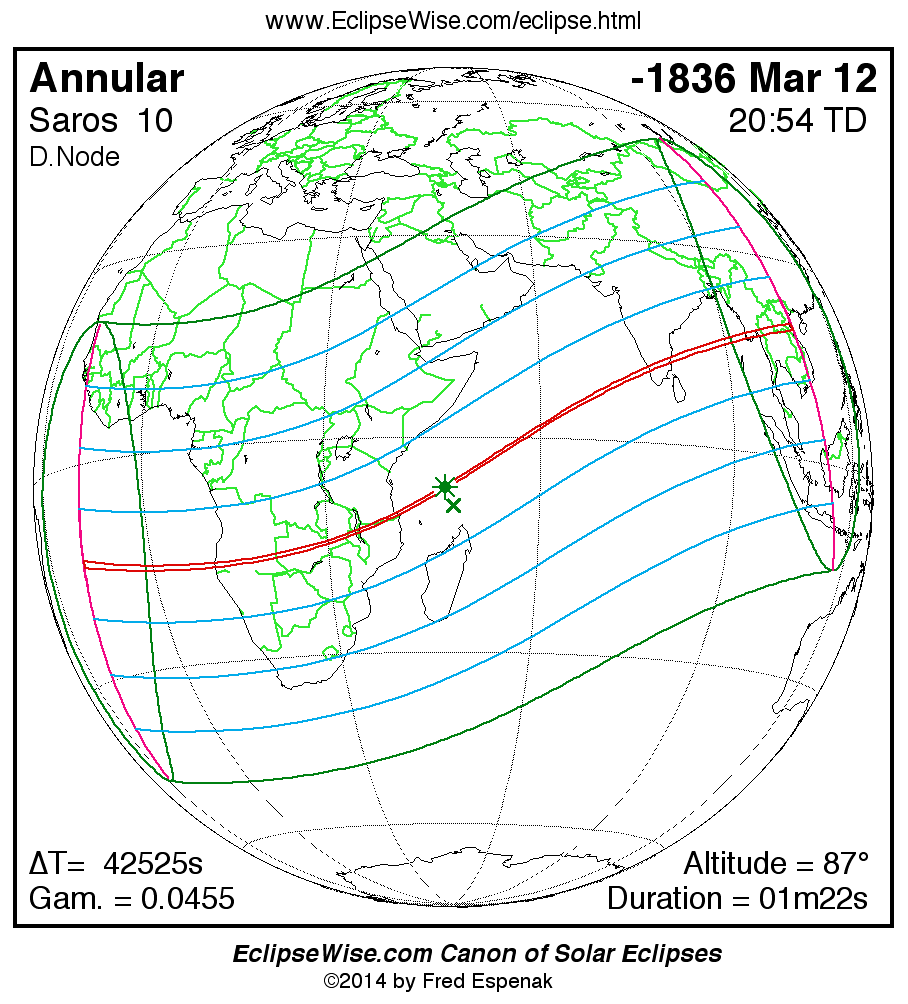
eclipse map

The Annular Solar Eclipse of -1836 Mar 12 (1837 Mar 12 BCE) is visible from the geographic regions shown on the map to the right. Click on the map to enlarge it. For an explanation of the features appearing in the map, see Key to Solar Eclipse Maps.

The instant of greatest eclipse takes place on -1836 Mar 12 at 20:54:17 TD (09:05:37 UT1). This is 6.3 days before the Moon reaches apogee. During the eclipse, the Sun is in the constellation Aries. The synodic month in which the eclipse takes place has a Brown Lunation Number of -46490.

The eclipse belongs to Saros 10 and is number 36 of 73 eclipses in the series. All eclipses in this series occur at the Moon’s descending node. The Moon moves northward with respect to the node with each succeeding eclipse in the series and gamma increases.

The annular solar eclipse of -1836 Mar 12 is preceded two weeks earlier by a penumbral lunar eclipse on -1836 Feb 27, and it is followed two weeks later by a penumbral lunar eclipse on -1836 Mar 28.

These eclipses all take place during a single eclipse season.

The eclipse predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 42519.9 seconds for this eclipse. The uncertainty in ΔT is 3071.1 seconds corresponding to a standard error in longitude of the eclipse path of ± 12.83°.

The following links provide maps and data for the eclipse.

The tables below contain detailed predictions and additional information on the Annular Solar Eclipse of -1836 Mar 12 .

Eclipse Data: Annular Solar Eclipse of -1836 Mar 12

Eclipse Characteristics
Parameter Value
Eclipse Magnitude 0.98797
Eclipse Obscuration 0.97608
Gamma 0.04557
Conjunction Times
Event Calendar Date and Time Julian Date
Greatest Eclipse -1836 Mar 12 at 20:54:16.8 TD (09:05:36.9 UT1) 1050529.878899
Ecliptic Conjunction -1836 Mar 12 at 20:53:46.0 TD (09:05:06.1 UT1) 1050529.878542
Equatorial Conjunction -1836 Mar 12 at 20:55:47.2 TD (09:07:07.3 UT1) 1050529.879945
Geocentric Coordinates of Sun and Moon
-1836 Mar 12 at 20:54:16.8 TD (09:05:36.9 UT1)
Coordinate Sun Moon
Right Ascension22h32m44.5s22h32m41.5s
Declination-09°21'06.3"-09°18'38.3"
Semi-Diameter 15'51.5" 15'25.4"
Eq. Hor. Parallax 08.7" 0°56'36.1"
Geocentric Libration of Moon
Angle Value
l 5.5°
b 0.1°
c -23.7°
Prediction Paramaters
Paramater Value
Ephemerides JPL DE406
ΔT 42519.9 s
k (penumbra) 0.2725076
k (umbra) 0.2722810
Saros Series 10 (36/73)

Explanation of Solar Eclipse Data Tables

Penumbral Shadow Contacts and Extremes: Annular Solar Eclipse of -1836 Mar 12

Contacts of Penumbral Shadow with Earth
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
First External ContactP117:59:46.406:11:06.514°35.2'S001°12.8'W
First Internal ContactP220:04:26.308:15:46.410°26.9'S031°39.8'W
Last Internal ContactP321:44:03.709:55:23.822°05.5'N121°20.3'E
Last External ContactP423:48:52.812:00:12.817°57.2'N090°54.4'E
Extreme Northern and Southern Path Limits of Penumbra
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
North Extreme Path Limit 1N119:19:58.807:31:18.820°12.5'N015°19.2'W
South Extreme Path Limit 1S119:21:41.607:33:01.746°17.5'S029°10.6'W
North Extreme Path Limit 2N222:28:15.910:39:36.052°25.8'N101°46.9'E
South Extreme Path Limit 2S222:27:07.410:38:27.514°00.3'S116°44.7'E

Explanation of Penumbral Shadow Contacts and Extremes Tables

Umbral Shadow Contacts and Extremes: Annular Solar Eclipse of -1836 Mar 12

Contacts of Umbral Shadow with Earth
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
First External ContactU119:01:10.607:12:30.713°41.3'S016°24.4'W
First Internal ContactU219:02:54.407:14:14.513°38.9'S016°50.0'W
Last Internal ContactU322:45:36.010:56:56.118°53.5'N106°33.3'E
Last External ContactU422:47:25.510:58:45.618°51.0'N106°06.4'E
Extreme Northern and Southern Path Limits of Umbra
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
North Extreme Path Limit 1N119:02:00.707:13:20.813°14.0'S016°32.2'W
South Extreme Path Limit 1S119:02:04.507:13:24.514°06.3'S016°42.3'W
North Extreme Path Limit 2N222:46:32.410:57:52.519°19.8'N106°14.4'E
South Extreme Path Limit 2S222:46:28.910:57:49.018°24.7'N106°25.4'E

Explanation of Umbral Shadow Contacts and Extremes Tables

Central Line Extremes and Duration: Annular Solar Eclipse of -1836 Mar 12

Extreme Limits of the Central Line
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
Extreme Central Line Limit 1C119:02:02.507:13:22.613°40.1'S016°37.2'W
Extreme Central Line Limit 2C222:46:30.810:57:50.818°52.2'N106°19.9'E

Explanation of Central Line Extremes Table

Greatest Eclipse and Greatest Duration
Event Time
TD		 Time
UT1		 Latitude Longitude Sun
Altitude		 Sun
Azimuth		 Path Width Central
Duration
Greatest Eclipse20:54:16.809:05:36.906°53.5'S130°46.8'W 87.4° 163.4° 42.5 km01m21.57s
Greatest Duration22:46:30.810:57:50.818°52.2'N106°19.9'E 0.0° 260.1° 103.5 km01m49.38s

Explanation of Greatest Eclipse and Greatest Duration

Polynomial Besselian Elements: Annular Solar Eclipse of -1836 Mar 12

Polynomial Besselian Elements
-1836 Mar 12 at 21:00:00.0 TD (=t0)
n x y d l1 l2 μ
0 0.03597 0.05809 -9.3504 0.55414 0.00794 131.4674
1 0.51220 0.15070 0.0148 0.00011 0.00011 15.0044
2 -0.00003 0.00004 0.0000 -0.00001 -0.00001 0.0000
3 -0.00001 -0.00000 - - - -
Tan ƒ1 0.0046367
Tan ƒ2 0.0046136

At time t1 (decimal hours), each besselian element is evaluated by:

x = x0 + x1*t + x2*t2 + x3*t3 (or x = Σ [xn*tn]; n = 0 to 3)

where: t = t1 - t0 (decimal hours) and t0 = 21.000

Explanation of Polynomial Besselian Elements

Links for the Annular Solar Eclipse of -1836 Mar 12 (1837 Mar 12 BCE)

Links to Additional Solar Eclipse Information

Calendar

The Gregorian calendar (also called the Western calendar) is internationally the most widely used civil calendar. It is named for Pope Gregory XIII, who introduced it in 1582. On this website, the Gregorian calendar is used for all calendar dates from 1582 Oct 15 onwards. Before that date, the Julian calendar is used. For more information on this topic, see Calendar Dates.

The Julian calendar does not include the year 0. Thus the year 1 BCE is followed by the year 1 CE (See: BCE/CE Dating Conventions). This is awkward for arithmetic calculations. Years in this catalog are numbered astronomically and include the year 0. Historians should note there is a difference of one year between astronomical dates and BCE dates. Thus, the astronomical year 0 corresponds to 1 BCE, and astronomical year -1 corresponds to 2 BCE, etc..

Eclipse Predictions

Predictions for the Annular Solar Eclipse of -1836 Mar 12 were generated using the JPL DE406 solar and lunar ephemerides. The lunar coordinates were calculated with respect to the Moon's Center of Mass. The predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 42519.9 seconds for this eclipse. The uncertainty in ΔT is 3071.1 seconds corresponding to a standard error in longitude of the eclipse path of ± 12.83°.

Acknowledgments

Some of the content on this website is based on the book Thousand Year Canon of Solar Eclipses 1501 to 2500. All eclipse calculations are by Fred Espenak, and he assumes full responsibility for their accuracy.

Permission is granted to reproduce eclipse data when accompanied by a link to this page and an acknowledgment:

"Eclipse Predictions by Fred Espenak, www.EclipseWise.com"

The use of diagrams and maps is permitted provided that they are NOT altered (except for re-sizing) and the embedded credit line is NOT removed or covered.